The following is an illustration of how to solve a simple series circuit. Keep in mind that you should be familiar with all of the relationships of a series circuit which are:
- There is only one path for current in a series circuit.
- All the currents (I1, I2 .. In) are equal to It (the total current) in a series circuit.
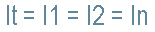
- The resistance total in a series circuit is

- The Voltage gain (Et) is equal to the sum of all the voltage drops (E1 + E2 + ... En)

- The power total dissipated in Watts in a series circuit is the sum of all power dissipated in the circuit.
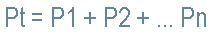
The basic steps for solving a series circuit problem are as follows:
- Draw the original series circuit.
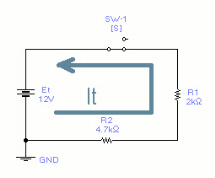
- Solve for resistance total (Rt) of the series circuit.

- Draw an equivalent circuit using the value of Rt.
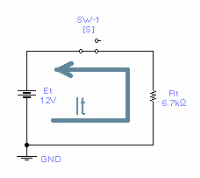
- Using Ohm's Law (I = E/R), solve for the total current (It) in the series circuit using the value of Rt and Et.
- Go back to your original drawing of your series circuit.
- Solve for each voltage drop using Ohm's Law E = I*R where the current in each case (I1) is equal to It.
Examples: E1 = I1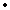 R1, E2 = I2 R1, E2 = I2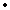 R2, etc. R2, etc.
- As a check, sum all of your voltage drops and they should equal the voltage gain (Et).

- Using Watt's Law P=I*E, solve for the power dissipated in each resistor.
Examples: P1 = I1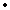 E1, P2 = I2 E1, P2 = I2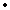 E2, etc. E2, etc.
- Sum the power dissipated in each resistor to attain the power total dissipated in the circuit.
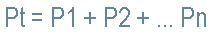
|