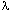 ): The length in space occupied by one cycle of a periodic wave.
): The length in space occupied by one cycle of a periodic wave.
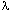 ): The length in space occupied by one cycle of a periodic wave.
): The length in space occupied by one cycle of a periodic wave.
|
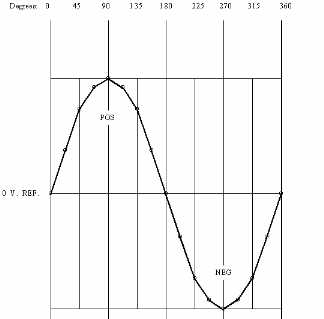
Alternating current continually changes in direction and size (amplitude) as shown in the picture on your left. The picture is that of a sine wave and it takes a specific time (t) to occur. The time it takes to occur in one second is called it's frequency (f). Frequency is measured in Hertz. First, let's consider the occurance of the wave pictured. If it took one second to go from 0 to maximum to 0, then from 0 to minimum to 0, it's frequency is 1 Hertz. If the wave were to take 0.20 seconds to occur, then it's frequency would be 5 Hertz. The formula for frequency (f) is 1/t , where t is time it takes for one full cycle to occur. Notice at the very top of the picture of the wave that there are several numbers. Those are the angular degrees of the wave. At specific points, we know what the size or amplitude will be due to the predictable nature of the wave. Some of the crucial spots are listed in the table below the picture. Pay particular attention to 0,180 and 360 degrees. One other measurement is important, the wavelength ( |